| Volume 31 Number 2 | Stony Brook, NY | < February 2019 > |
 |
|
|
New Publications

|
|
Synaptic Communication: Violins at the Super Bowl
James P. Dilger, PhD
I've been studying the violin recently. Actually, I've been looking at the violin plot, not the instrument. I've become a big fan! Okay, I know this sounds like a really nerdy topic, but try to stay with me. It all started with a project I was doing with the high school student Sarah Adamo (now a freshman at Northeastern U) whom I've written about before. Her experimental data on sea anemones was not normally (bell shaped curve) distributed. This required particular statistics (nonparametric) for analysis. That was not a problem. But the question was how to best display the results graphically to compare datasets.
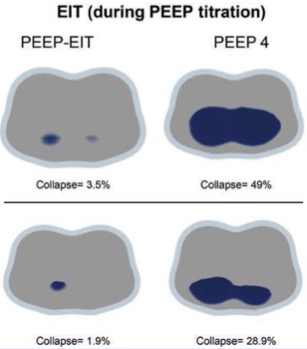
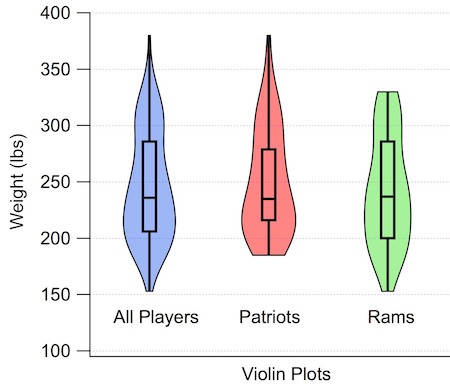
Rather than getting into the details of her data, let me illustrate this with something with decidedly international appeal. Let's consider the weights of the 106 players (53 on each team) on the active rosters of the two Super Bowl teams this year: New England Patriots and Los Angeles Rams. Here is a histogram showing the distribution of weights. This is most definitely not a bell-shaped curve! While the average is about 246 pounds, it ranges from 153 lbs (Rams' wide receiver JoJo Natson) to 380 lbs (Patriots' offensive tackle Trent Brown). Even I, a football agnostic, get the idea. Some players have to be nimble and quick, others have to resemble a brick wall. Stats people would say that the histogram is bimodal. 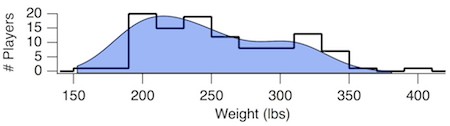
An alternative to the histogram is to plot each point along with a bar showing the median value (recall that there are as many points above the median as there are below). Because the average does not tell us too much, you might be inclined to include the standard error of the mean (SEM). As you can see, that's not useful at all. The standard deviation (SD) provides a bit more flavor of the wide range of values observed, but does not reflect the asymmetry of the distribution. In the 1970s, statistician John Tukey increased the information content when he introduced the Box and Whisker Plot. The top and bottom ends of the box represent the 25th and 75th percentiles of the distribution, the center line is the median (50th percentile) and the whiskers extend out to the full range of the dataset. Thus, our 106 data points can been reduced to five descriptive numbers in an easy to understand graph. However, this still does not capture the bimodal nature of the distribution. 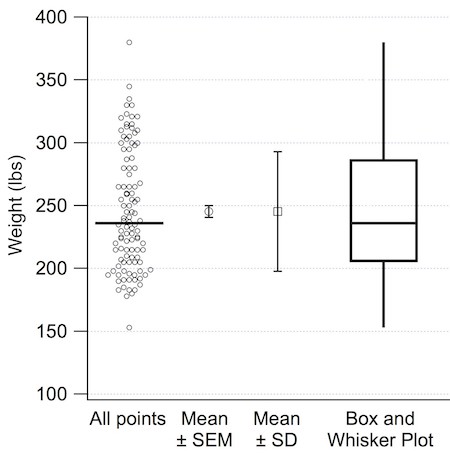

|
|
Where on Campus is That?
James P. Dilger, PhD

|
|
Monthly Muscle Chillaxant



|
|
SleepTalker, the Stony Brook Anesthesiology Newsletter is published by the Department of Anesthesiology
Stony Brook Medicine, Stony Brook, NY Tong Joo Gan, M.D., Chairman Editorial Board: James P. Dilger, Ph.D.; Stephen A. Vitkun, M.D., M.B.A., Ph.D.; Marisa Barone-Citrano, M.A.; Richard Tenure, M.D. |